2024金融工程报告：ASTGNN因子选股模型优化与应用

引言

随着机器学习学科的高速发展，以神经网络、决策树为主的机器学习模型在量化领域的应用受到相关研究人员的广泛关注，前期报告《基于循环神经网络的多频率因子挖掘》、《基于残差网络端到端因子挖掘模型》、《基于抗噪的AI量价模型改进方案》和《自适应图神经网络周频alpha模型》中，我们利用循环神经网络（RNN）、残差网络（ResNets）、自适应图神经网络（ASTGCN）和决策树模型搭建了端到端AI量价模型框架，这套框架的输入是个股最原始的K线数据比如高开低收换手率等，而最终的输出则是具有较强选股能力的alpha因子。我们将其该框架生成的因子应用于选股策略。回测结果显示该策略在样本外有着十分显著的选股效果。这套AI量价模型框架主要是基于多个不同频率数据集搭建的，这些数据集分别是周度（week）、日度（day）、分钟线（ms）和Level-2（l2）数据集。

其中周度和分钟线数据集我们分别是将每五个交易日日K线和每日半小时K线形成矩阵数据，然后将这些矩阵通过ResNets提取出相应时间频度的特征向量，接着将ResNets提取的特征向量按照时间先后输入到RNN模型中进行时序学习，最终获得相应数据集的alpha因子。数据集day则是直接将预处理好的日K线数据通过RNN模型提取出相应的alpha因子。四个数据集中只有Level-2则是将原始数据通过人工合成成日频因子的方式形成的。整个AI量价模型框架分为三个部分，数据预处理、提取因子单元、因子单元动态加权。数据预处理包括去极值、标准化和补充缺失值三个步骤，而提取因子单元则是通过将预处理好后的特征或者残差网络提取得到的特征通过RNN和图模型转化成一系列具有一定选股能力的弱因子，因子加权则是利用决策树对这些不同数据集上生成的弱因子进行短周期非线性加权形成模型最终的个股得分，部分整个流程如下图所示：

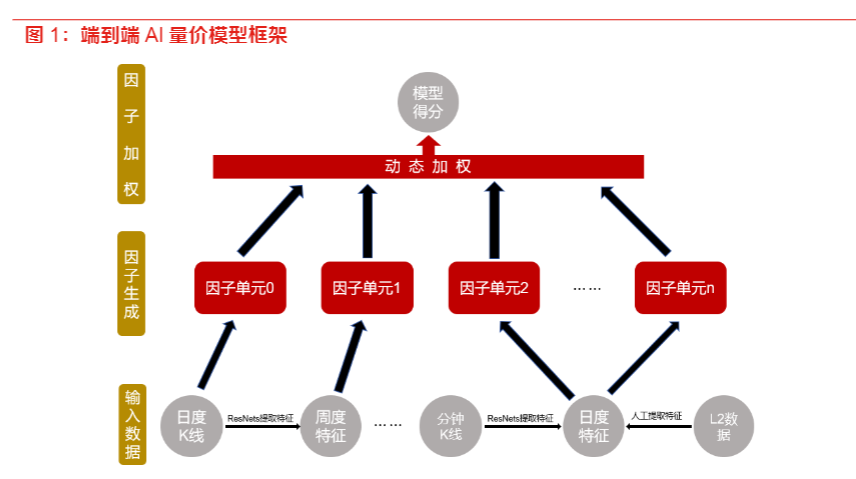
该端到端AI量价模型框架的因子单元提取阶段，我们借助RNN模型强大的时序提取能力，将输入的时间序列数据加工成含有时序信息的截面特征，最后利用图模型来考虑交易日截面个股之间的关联关系，最终得到我们所需的因子单元。

我们使用的图模型区别于传统模型，即不再使用先验信息来构建邻接矩阵，完全根据输入数据学习出短期个股的交互关系，利用两支RNN模型来进行学习，其中一支RNN模型（称为主GRU）用于生成图模型的输入，而根据另外一支RNN模型（称为次GRU）的输出来计算个股之间的交互关系（即邻接矩阵）。由于我们在训练的时候损失函数部分没有考虑到生成邻接矩阵的RNN模型，因此我们学习到的邻接矩阵可能存在一些缺陷：1.由于我们是将次RNN模型输出的个股特征来刻画个股“属性”，并利用这种“属性”来计算个股之间的相似度从而获取个股的邻接矩阵，但如果不对次GRU进行约束，可能导致所生成的特征对个股“属性”刻画比较粗糙从而使得邻接矩阵对个股相似度刻画“准确性”大打折扣。

2.邻接矩阵代表股票间的关联关系，如果邻接矩阵变化速度过快，将会在导致模型最终生成因子换手率大幅提高，这意味着实盘中将付出更多的交易费用，另外一方面不对邻接矩阵自相关系数进行控制会导致在训练过程中更多学习到数据中的噪声，从而使得邻接矩阵鲁棒性下降，模型更加容易过拟合。另一方面，一些长周期量价因子或者低频基本面因子对短周期预测能够起到一定的帮助，这部分数据蕴含的alpha信息往往与短周期量价数据的alpha信息相关性更低，使全模型获得更多信息增量。综合上述几个角度，本文将对原有的模型框架进行改进，以期能够让全模型的选股效果获得更大的提升。

一、融入基本面信息的ASTGNN模型

这一章我们将介绍融入基本面信息的ASTGNN模型，基本面信息的融入主要有两种方式：1.通过给神经网络输入一些量价与基本面数据让神经网络自助学习出一些风险因子，再利用这些风险因子构建图模型中的邻接矩阵；2.则是通过将一些基本面因子构建成数据集，通过RNN和DNN提取出因子单元，从而能和原始量价数据集的因子单元形成信息互补。下面我们将分别介绍这两种改进方案。

1.1图模型邻接矩阵的改进

前期报告《自适应时空图网络周频alpha模型》中，我们采用两支GRU模型的方式，利用相同的输入分别提取个股的属性特征向量和alpha因子特征向量（生成属性特征向量的GRU我们称次GRU，生成alpha因子特征向量的GRU我们称之为主GRU），最终形成自适应图模型的邻接矩阵和输入。这种方式虽然有助于区分相同股票提取出的属性信息和alpha信息，但是由于我们在模型阶段没有对生成属性特征的GRU进行限制，因而很可能两个GRU提取出来信息之间的重叠度仍然较高。为了应对上述问题，我们使用RNN+GAT网络来提取属性特征向量（记为𝑭），该网络具体结构可表示为如下形式

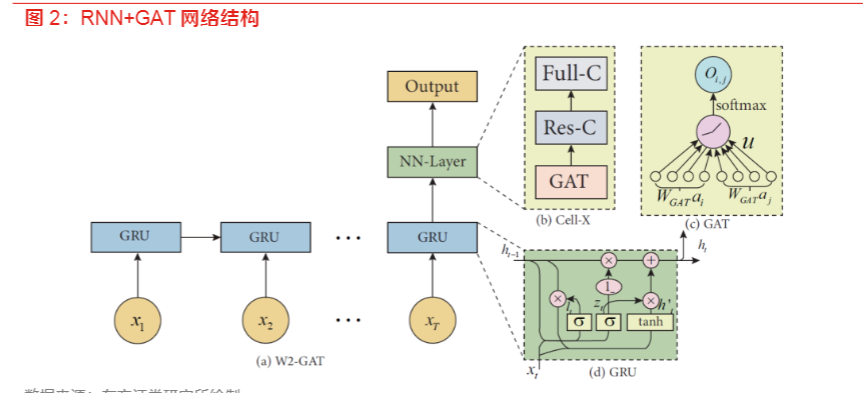
上图中GAT为图注意力机制，Res-C表示残差连接，Full-C表示全连接变换加Batch-norm层，并且我们还将该部分网络的损失函数进行改进。输入端主要由基础数据和Barra十个因子构成，而新设计的损失函数主要由两部分构成:第一部分，我们希望相似股票在未来能有相似的表现，因此损失函数第一项我们构造属性特征向量与未来t期截面标准化之后的收益率（记为𝑦𝑡）之间的R-square。并且我们希望邻接矩阵随时间变化程度不会过大（变化过大造成前后两期股票间依赖关系变化较大，从而最终全模型生成的alpha因子换手率可能会较大）。

第二部分，我们希望属性特征向量各分量之间信息重叠度尽可能低，为了达到这个目标，我们引入相关系数矩阵范数的正交惩罚项作为损失函数第二项。综合上述结果，我们最终设计损失函数可表示为：∑𝜔𝑡−1R−square(𝑭,𝑦𝑡)𝑇𝑡=1+λ||corr(𝑭,𝑭)||2其中参数𝜔表示属性特征向量与未来t期标准收益率（记为𝑦𝑡）之间的R-square的权重，并且0<𝜔<1（即t越大则该期计算所得R-square损失对应权重越小）。参数λ表示相关系数惩罚项权重系数，是一个人为确定的超参数。上述损失函数中R-square具体计算方式可以由以下公式给出：R−square(𝑭,𝑦𝑡)=1−||𝑦𝑡−𝑭(𝑭𝑻𝑭)−𝟏𝑭𝑻𝑦𝑡||。而RNN+GAT模型的输入则主要是一些长周期风险因子构成，这些风险因子主要分为十个大类，具体组成如下图所示：

上述结果可以看出除分量f9自相关系数外，其余分量自相关系数都高于91%，这意味着对于周频而言通过加入滞后多期R-square作为损失函数惩罚项后，前后两期股票“属性”变化不大，相似度值也变化较小。我们因子单元提取的网络结构中图模型部分可表示为以下两种形式：𝒁=(𝑰+𝑠𝑜𝑓𝑡𝑚𝑎𝑥(𝑅𝑒𝐿𝑈(𝑴𝑴𝑻)))𝑿𝑾（加法）𝒁=(𝑰−𝑠𝑜𝑓𝑡𝑚𝑎𝑥(𝑅𝑒𝐿𝑈(𝑴𝑴𝑻)))𝑿𝑾（减法）这里加法方式表示利用同类型股票来进行对股票自身alpha特征进行加强，可以理解为一种动量效应。而减法则可以理解为通过同类型的股票来进行中性化。整个因子单元提取的网络结构示意图可表示为：

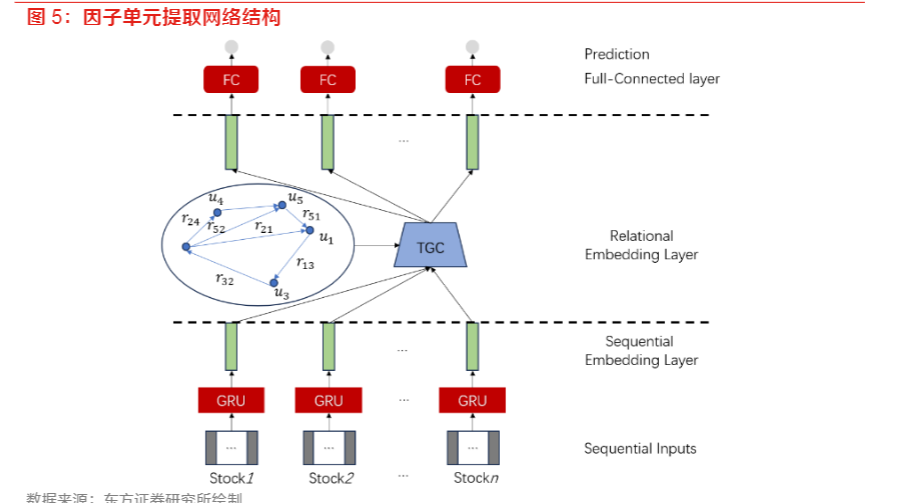
1.2加入基本面数据集

考虑到本模型生成的机器学习因子获得的超额收益有相当一部分来自于行业风格轮动，而长期动量、长期波动等风险因子能够协助模型更好的捕捉这一部分收益，且这些风险因子与我们模型中周度、日度、分钟线和l2数据集生成因子相关性不高，可以产生信息增量，因此我们构建长周期基本面数据集lfq。

长周期基本面数据集中的基本面特征主要由以下几类因子组成：➢估值类：EP（扣非净利润TTM/市值）、EPTTM滚动一年zscore、DP（过去一年分红/总市值）；➢成长类：扣非后净利润同比增速、净资产收益率（ROE）；➢超预期类：SUE因子；➢确定性类：公募基金持仓比例、分析师覆盖度；为了克服基本面数据离群值较多，分布极其不正态等问题，我们采用了报告《基本面因子重构》中的处理方式进行回归，并且采用了与量价类数据集不同的预处理方法来促进神经网络更好的从基本面数据集中有效的提取alpha信息。对于长周期风险因子，许多因子取值隔日变化较小，相邻两天数据变化不大但收益率构建的标签可能发生比较大的变化，因此使用RNN模型很难提取出较为有效的时序信息，且容易使得RNN模型本身对数据微小扰动变得较为敏感。

通过上述结果，我们可以得到：1.两个数据集生成因子的选股表现均较好，并且lfq_daily数据集生成因子的表现整体强于lfq_monthly数据集，但lfq_monthly数据集多头组合换手率明显更低。2.两个数据集生成因子选股能力没有出现衰减迹象，但整体表现呈现出明显的周期变化趋势，即奇数年超额相对较低而偶数年超额则相对更高。3.两种采样方式下生成因子相关性较低仅仅只有46.80%，但暴露情况大致相同，主要是在波动和估值这两种风格上暴露程度较大。相对于月频采样，日频采样生成因子在非线性市值（CubicSize）上暴露相对更大而在趋势（Trend）上相对更小。

今年以来，月度采样的长周期数据集表现明显好于日频采样。截至2024年4月30日，该数据集生成因子在沪深300上双周频RankIC均值为12.82%，分5组top组超额收益率为12.26%，超额收益的最大回撤仅-1.50%；在中证500上RankIC均值为9.39%，分5组top组超额收益率为10.89%，超额收益的最大回撤-4.33%；在中证1000上RankIC均值为16.08%，分5组top组超额收益率为17.03%，超额收益的最大回撤仅-2.85%。

二、各数据集单因子分析

2.1回测说明

第二、三章的回测结果中，各项指标计算方法如下所示：1. RankIC均值是当天因子与隔日未来十日收益率（即T+1~T+11收盘）序列进行计算的，并且每隔十个交易日计算一次，最终将这个RankIC序列取平均得到的。2. ICIR则是根据上述RankIC序列均值除以序列标准差计算得到的。3. 分组测试结果中，top组和bottom组对冲年化收益（中证全指股票池上我们是将股票池分成20组，而沪深300、中证500和中证1000股票池上则是分成5组），周度调仓，次日收盘价成交并且不考虑交易成本计算得到的。4. 周均单边换手率是根据多头组持仓计算得到，而最大回撤和年化波动率则是根据top组超额收益净值计算得到的。

2.2各数据集单因子绩效分析

本节我们将对比week、day、ms、l2、lfq_daily和lfq_monthly这六个数据集上分别生成因子在中证全指股票池上的选股效果。通过上述图表结果，我们可以看出：1.整体来看，各个数据集中lfq_daily数据集表现最好，这说明基本面相关的数据集生成短期高频alpha因子可能拥挤度相对不高。2.今年以来截至2024年4月30日，各个数据集中，数据集week和lfq_monthly表现最好，超额收益均超过了20%，且最大回撤相对往年更低。3.今年以来截至2024年4月30日，相对于数据集day、ms和l2，数据集lfq_daily生成因子的超额收益更高且最大回撤相对更小。说明基本面数据确实带来了一些信息增量，从而使得数据集lfq_daily在今年有着更好的表现。

2.3各数据集单因子相关系数分析

长周期数据集与其他数据集相关性较低，其中lfq_monthly因子相关性均低于0.5，这意味着通过引入基本面可以给数据集带来信息增量，但日度采样的估值因子中包含了日度个股价格序列信息，在RNN进行时序学习的时候可能过度捕捉这一部分信息，最终导致最终生成因子与数据集day 和Ms 生成因子相关性相对较高。2.各数据集之间相关性均低于0.8，这说明数据集之间存在一定的信息差异，因而组合起来会产生信息互补作用，最终合成得到的综合打分相对单数据集有更强的选股效果。

2.4各数据集特征重要性分析

五个数据集贡献度最高的数据集是week数据集，而贡献程度最低的是l2数据集。事实上相较于其他几个数据集，l2数据信息含量更加丰富，与其他数据集之间的相关性也更低，因此l2数据集仍有较大改善空间。2.数据集week贡献度占比长期维持在30%左右，数据集day自2020年以来对综合打分的贡献程度占比持续下降，而数据集lfq对综合打分贡献程度占比持续上升。这可能和day数据集上拥挤度较高、alpha衰减较快有关，而对于低频数据集（比如week）拥挤度较低，alpha有效性相对较高，因而week数据集贡献度占比能够稳定维持在一个较高水平。

三、各数据集因子非线性加权结果分析

本章展示各数据生成弱因子经过非线性加权方法后得到最终因子在中证全指、沪深300、中证500和中证1000四个股票池中的表现。

上述结果按照因子取值大小进行分组，top组为因子取值最大组，通过上述图表结果我们可以看出：1.通过加入长周期数据集之后（加入lfq栏），因子RankIC、ICIR、因子多头和空头组超额显著提升，多头组的换手率也有所下降。这说明加入长周期数据集能够给全模型带来更多的信息增量，因而全模型选股效果能够进一步提升。2.通过引入机器学习风险因子来构建图模型的邻接矩阵后（减法和加法栏），因子RankIC、ICIR、因子多头和空头组超额能够得到进一步提升，而多头组合的换手情况也能进一步下降。说明使用机器学习风险因子来进行股票相似度的刻画更加精确。另外，经过测试合成打分直接用于月频也有着较好的选股效果，2018年和2020年以来截至2024年4月30日月频RankIC分别可达19.16%和17.53%，ICIR可达2.07和2.10，分二十组多头超额为35.03%和35.27%。通过引入未来二十日收益率作为标签以及将输入RNN模型序列长度拉长能够进一步提升该框架在月频上的表现。

3.2各宽基指数上的表现

通过以上结果我们可以看出各个模型生成因子的市值偏向性较低，在各个股票池上都有较强的选股能力。并且通过加入长周期数据集和引入风险因子构建图模型的邻接矩阵，所生成因子在各宽基指数上的RankIC和ICIR等指标能够进一步得到提升。

四、合成因子指数增强组合表现

4.1增强组合构建说明

本章将展示了减法模型下各数据集非线性加权得分在沪深300、中证500和中证1000指数增强的应用效果，关于指数增强组合有如下说明：1）回测期20171229~20240430，组合周频调仓，假设根据每周五个股得分在次日以vwap 价格进行交易，股票池为中证全指成分股。2）风险因子库dfrisk2020（参见《东方A股因子风险模型（DFQ-2020）》）的所有风格因子相对暴露不超过0.5，所有行业因子相对暴露不超过2%，中证500 增强跟踪误差约束不超过5%，沪深300 增强跟踪误差约束不超过4%。3）指增策略组合构建时，限制指数成分股占比，成分股占比约束记为cpct（cpct=None表示成分股占比不进行约束，cpct=0.8表示成分股占比进行80%约束，cpct=1表示成分股占比进行100%约束），周单边换手率限制记为delta。4）组合业绩测算时假设买入成本千分之一、卖出成本千分之二，停牌和涨停不能买入、停牌和跌停不能卖出。

（本文仅供参考，不代表我们的任何投资建议。如需使用相关信息，请参阅报告原文。）