2024期货市场择时模型:基于幂律特征的策略分析
1、复杂系统的幂律特征
幂律出现在许多领域。许多系统在变大时表现出分形结构,当人们观察越来越大的系统时,描述它们行为的规则在重新缩放时看起来是一样的。连续相变(如铁磁体中的居里点)、无序系统的动力学行为(脱钉跃迁、爆裂噪声和雪崩)、混沌的开始、地震、充分发展的湍流以及股票市场的行为都显示出涌现尺度不变性的明显特征,并且都在其行为的各种度量中表现出幂律。
在许多这样的系统中,这些幂律是使用重整化群(RG)来解释的,粗粒化一个系统,然后重新缩放(重整)参数和观测量以达到一个固定点。在某些系统(湍流、地震)中,几乎有一个共识。在其他系统中,存在通用临界指数和通用标度函数,没有已知的RG解释。重整化群预言了与各种量相关的幂律,这些量是普适的。
许多系统随着尺度变大,从一个幂律平滑地过渡到另一个幂律,通常观察到出现在有限温度下的量子临界点。在相变点附近,各类物理量显示出显著的幂律(power-law)行为。在金融市场中,我们基于复杂系统的幂律特征,尝试构建了市场变盘点的择时模型。
2、幂律分布的相关原理
2.1、幂律分布与无标度现象
1932年,哈佛大学的语言学专家Zipf在研究英文单词出现的频率时,发现如果把单词出现的频率按由大到小的顺序排列,则每个单词出现的频率与它的名次的常数次幂存在简单的反比关系。19世纪的意大利经济学家Pareto研究了个人收入的统计分布,发现少数人的收入要远多于大多数人的收入,提出了著名的二八法则。Zipf定律与Pareto定律都是简单的幂函数,我们称之为幂律分布。
幂律分布广泛存在于物理学、地球与行星科学、生物学、经济与金融学等众多领域中,且表现形式多种多样,包括地震规模大小的分布、网页被点击次数的分布、书籍及唱片的销售册数或张数的分布、每类生物中物种数的分布等都是典型的幂律分布。
统计物理学家习惯于把服从幂律分布的现象称为无标度现象,即系统中个体的尺度相差悬殊,缺乏一个优选的规模。凡有生命的地方,有进化、有竞争的地方都会出现不同程度的无标度现象。
2.2、无标度网络与幂律
近些年,复杂网络的研究越来越热门。钱学森曾给出了复杂网络的一个较严格的定义:具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络。无标度网络(scalefree network)是A.-L. Barabasi在1999年提出的概念,A.-L. Barabasi将这些网络命名为无标度网络,灵感来自于在相变附近观察到的幂律的无标度性质。
无标度网络中其各节点之间的连接状况(度数)具有严重的不均匀分布性。网络中少数称之为Hub点的节点拥有绝对多数的连接,而大多数节点只有很少量的连接。少数Hub点对无标度网络的运行起着主导的作用。因特网和代谢网的度分布虽然为幂律,但却是标度丰富的两个典型案例,它们面对蓄意攻击仍然“稳健而非脆弱”。
2000年,Barabasi等人用随机网络和无标度网络进行对比研究,讨论了节点随机失效和被有意图攻击的不同结果。ALBERT R等人在《Error and attack tolerance of complex networks》通过模拟比较了ER随机图和BA无标度网对节点删除的影响。对ER随机图,随机失效和蓄意攻击没有区别;但对无标度网络,随机失效和蓄意攻击显著不同。ALBERT R等人认为是ER随机图节点同质而BA无标度网节点异质,即存在hub nodes所致。“稳健而又脆弱”是否为无标度网的普适特性?LI L等人在《Towards a theory of scale-free graphs: definitions, properties, and implications》给予了否定的回答。
无标度网络的度分布是一个非整数指数关系,这种网络的拓扑图呈现分形特征。幂律分布与分形、非线性、复杂性密切相关,它支配了所有自然演化的具有自相似特性的无标度网络。爱因斯坦曾说过,“要使我们的理论尽可能的简单——但不是更简单”。普适简单的幂律,告诉我们大自然是如此的复杂,而支配它的物理定律却又是如此的简洁优雅。
2.3、幂律分布的检验布
鲁克海文实验室的Bak、加州大学圣巴巴拉分校的汤超和佐治亚理工学院的Wiesenfeld等人用著名的沙堆模型皆阐明了自组织临界态的特点。幂律分布是自组织临界系统在混沌边缘,即从稳态过渡到混沌态的一个标志,利用它可以预测这类系统的相位及相变。自组织临界理论可以解释诸如火山爆发、山体滑坡以及金融市场中的幂律分布现象。借鉴幂律分布的特征,理论上可以识别金融市场的变盘点,一般的检验方法为Kolmogorov-Smirnov检验(KS检验)。KS检验以Andrey Kolmogorov和Nikolai Smirnov的名字命名。
3、利用复杂系统幂律特征择时的实证
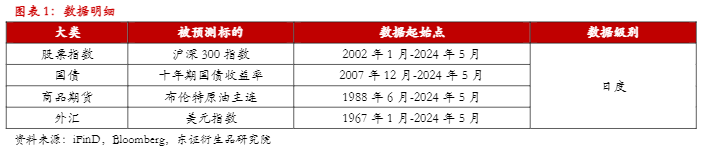
3.1、数据及其说明
在实证部分,我们选取的资产标的为沪深300指数、十年期国债收益率、美元指数和布伦特原油主连。数据明细说明如下表所示。
3.2、测试的流程及参数说明
测试的流程简化如下:
首先,提取资产的价格或者收益率日度时间序列;其次,根据上面给出的时间序列数据计算KS检验统计量D;最后,根据KS检验统计量D的斜率正负变化确定幂律特征变化所揭示的变盘点,依据行情序列的斜率确定变盘点之后的趋势方向,按照此规则测试沪深300指数、十年期国债收益率、布伦特原油主连、美元指数的择时效果。
测试过程中的参数说明:
第一,KS检验统计量D计算的窗口为144或者233个交易日,和我们过往撰写的复杂系统相关的报告遵循相同的原则,详情可参阅《基于复杂系统本征微观态的择时模型》等报告,参数为大于100的斐波那契序列;
第二,KS检验统计量D时间序列的斜率参数为13、21、34、55、89个交易日,参数为小于100的斐波那契序列,斜率的符号代表趋势方向,斜率的符号发生变化则记为“变盘点”,下一个“变盘点”就是“离场点”,行情序列的斜率参数为10个交易日;
第三,在测试过程中,进场方向有多有空,假设测试的标的均可做空。
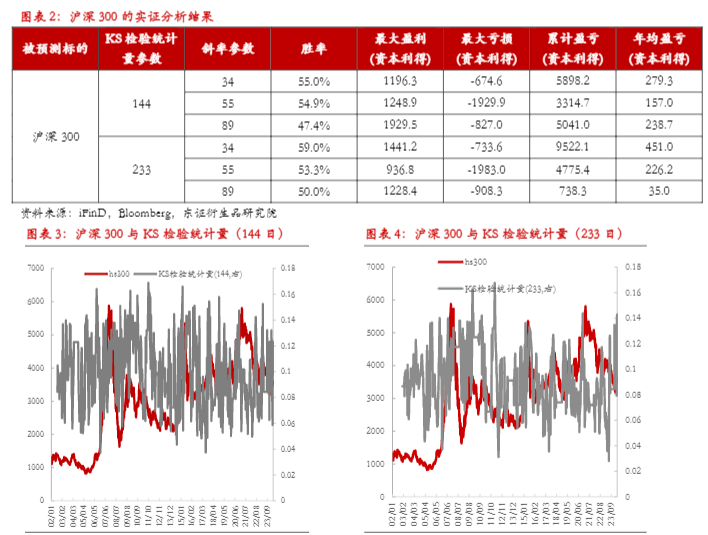
3.3、幂律特征的择时测试
在实证部分,我们测试的对象分别是沪深300指数、十年期国债收益率、布伦特原油主连、美元指数共四组,每组按照斜率参数可划分为多个测试情形。在《从因果涌现的视角挖掘择时模型》中因果涌现的量化指标涉及KL散度的计算,与这里关于复杂系统幂律特征的测试思路类似,从概率分布的差异这个角度构建变盘模型是符合逻辑直觉的。
(本文仅供参考,不代表我们的任何投资建议。如需使用相关信息,请参阅报告原文。)